该文章参考于: 点击链接
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
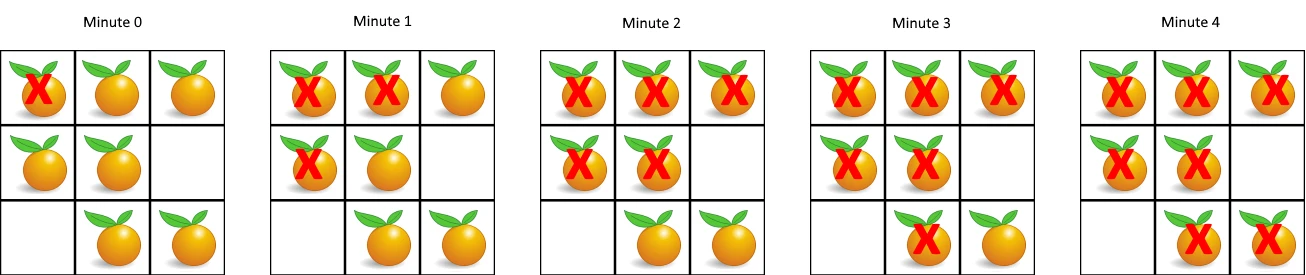
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
**解释:**左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]仅为0、1或2
题解
class Solution {
private static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 四方向
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int fresh = 0;
List<int[]> q = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
fresh++; // 统计新鲜橘子个数
} else if (grid[i][j] == 2) {
q.add(new int[]{i, j}); // 一开始就腐烂的橘子
}
}
}
int ans = 0;
while (fresh > 0 && !q.isEmpty()) {
ans++; // 经过一分钟
List<int[]> tmp = q;
q = new ArrayList<>();
for (int[] pos : tmp) { // 已经腐烂的橘子
for (int[] d : DIRECTIONS) { // 四方向
int i = pos[0] + d[0];
int j = pos[1] + d[1];
// 确保不超过边界
if (0 <= i && i < m && 0 <= j && j < n && grid[i][j] == 1) { // 新鲜橘子
fresh--;
grid[i][j] = 2; // 变成腐烂橘子
q.add(new int[]{i, j});
}
}
}
}
return fresh > 0 ? -1 : ans;
}
}
代码中使用了临时数组,占用空间过大,优化如下:
class Solution {
private static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 四方向
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int fresh = 0;
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
fresh++; // 统计新鲜橘子个数
} else if (grid[i][j] == 2) {
queue.add(new int[]{i, j}); // 一开始就腐烂的橘子
}
}
}
int ans = 0;
while (fresh > 0 && !queue.isEmpty()) {
ans++; // 经过一分钟
int count = queue.size();
for (int k = 0; k < count; k++) { // 已经腐烂的橘子
int[] pos = queue.poll();
for (int[] d : DIRECTIONS) { // 四方向
int i = pos[0] + d[0];
int j = pos[1] + d[1];
if (0 <= i && i < m && 0 <= j && j < n && grid[i][j] == 1) { // 新鲜橘子
fresh--;
grid[i][j] = 2; // 变成腐烂橘子
queue.add(new int[]{i, j});
}
}
}
}
return fresh > 0 ? -1 : ans;
}
}
更进一步的优化方案:避免重复创建 int[] 数组(使用更紧凑的编码方式)
在 BFS 中,你每次用 new int[]{i, j} 来表示坐标。这会频繁创建小对象,虽然 Java 有 GC,但在小规模网格(最多 10x10=100 个格子)中,仍可通过将坐标编码为单个整数来减少对象分配开销。
优化点:用 i * n + j 编码坐标,入队时存整数,出队时解码。
这是 BFS 中常见的空间/性能优化技巧,尤其在小网格中能略微提升速度并减少 GC 压力。
class Solution {
private static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int fresh = 0;
Queue<Integer> queue = new LinkedList<>(); // 存储编码后的坐标:i * n + j
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
fresh++;
} else if (grid[i][j] == 2) {
queue.offer(i * n + j); // 编码入队
}
}
}
int ans = 0;
while (fresh > 0 && !queue.isEmpty()) {
ans++;
int size = queue.size();
for (int k = 0; k < size; k++) {
int code = queue.poll();
int i = code / n; // 解码行
int j = code % n; // 解码列
for (int[] d : DIRECTIONS) {
int ni = i + d[0];
int nj = j + d[1];
if (ni >= 0 && ni < m && nj >= 0 && nj < n && grid[ni][nj] == 1) {
fresh--;
grid[ni][nj] = 2;
queue.offer(ni * n + nj); // 编码入队
}
}
}
}
return fresh == 0 ? ans : -1;
}
}
✅ 优化效果说明:
- 减少对象分配:不再频繁创建
int[2]数组。 - 内存更紧凑:
Integer比int[]占用更少堆内存(尤其在小数据下)。 - 速度提升:虽然在 LeetCode 小数据上可能不明显,但这是标准 BFS 优化手段。
✅ 第 2 步优化:使用数组模拟队列(Array-based Queue)替代 LinkedList
由于题目中网格最大为 10x10 = 100 个单元格,腐烂橘子最多也就 100 个,BFS 队列长度上限非常小(≤100)。
而 LinkedList 作为队列,每次 offer/poll 都涉及对象包装(Integer)和链表节点操作,有一定开销。
优化点:用固定大小的数组 + 双指针(head/tail) 手动实现一个循环队列(ring buffer),避免对象装箱和链表开销。
这在小规模 BFS 中能显著减少常数时间开销,是竞赛常用技巧。
class Solution {
private static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int fresh = 0;
// 最多 m*n 个格子,全部腐烂也最多入队一次
int[] queue = new int[m * n]; // 存储编码坐标 i * n + j
int head = 0, tail = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
fresh++;
} else if (grid[i][j] == 2) {
queue[tail++] = i * n + j; // 入队
}
}
}
int ans = 0;
while (fresh > 0 && head < tail) {
ans++;
int size = tail - head; // 当前层的元素个数
for (int k = 0; k < size; k++) {
int code = queue[head++]; // 出队
int i = code / n;
int j = code % n;
for (int[] d : DIRECTIONS) {
int ni = i + d[0];
int nj = j + d[1];
if (ni >= 0 && ni < m && nj >= 0 && nj < n && grid[ni][nj] == 1) {
fresh--;
grid[ni][nj] = 2;
queue[tail++] = ni * n + nj; // 入队
}
}
}
}
return fresh == 0 ? ans : -1;
}
}
✅ 优化效果说明:
- 零对象分配:队列使用原始
int[],无Integer装箱/拆箱。 - 缓存友好:数组连续内存访问,比链表更快。
- 常数级加速:在 LeetCode 的小输入下,这种优化往往能从 1ms 降到 0ms(或稳定 0ms)。